摘要:权函数计算是一种重要的数学工具,涉及概念理解、应用和实践。它主要通过对特定数据赋予权重,以反映数据的重要性和相关性。权函数广泛应用于统计学、机器学习、信号处理等领域,用于数据处理、模型优化等任务。本文介绍了权函数的基本概念,详细阐述了其在实际中的应用,并通过实践案例展示了权函数计算的方法和效果。
导读
权函数是描述数据集中每个数据点对总体影响程度的数学工具,广泛应用于统计学、物理学、工程学等领域,本文将详细介绍权函数的基本概念、计算方法及其在实际应用中的价值。
权函数的基本概念
权函数,又称为权重函数,是一种用于描述数据集中每个数据点对总体影响的程度的数学工具,在统计学中,权函数常用于加权最小二乘法、加权回归等分析方法中,权函数的取值范围通常为0到无穷大之间,其中较大的权重表示对应的数据点对总体影响更大,通过引入权函数,我们可以更准确地描述数据集中各数据点的实际价值。
权函数的计算方法
权函数的计算通常依赖于具体的应用场景和数据集的特点,常见的计算步骤包括:
1、数据预处理:对原始数据进行清洗、缺失值填充等处理。
2、确定权重因子:根据数据集的特点和实际需求,确定权重因子,如数据点的频率、重要性等。
3、计算权函数值:根据权重因子和权函数的定义,计算每个数据点的权函数值,常见的权函数形式包括三角权函数、高斯权函数等。
权函数的应用
权函数在实际应用中具有广泛的应用价值,以下是一些常见的应用场景:
1、数据分析:通过引入权函数,可以更加准确地描述数据集中各数据点的实际价值,提高分析的准确性,在市场调研中,不同年龄段、不同职业的消费者对产品的关注度可能存在差异,通过引入权函数,可以更加准确地分析消费者的需求和行为。
2、机器学习:在机器学习中,权函数用于优化模型的训练过程,在神经网络中,通过调整不同数据点的权重,可以使模型更加关注重要数据点,从而提高模型的性能,权函数还可用于处理不平衡数据集,提高模型的泛化能力。
3、信号处理:权函数在滤波、插值等操作中发挥着重要作用,在音频信号处理中,通过引入权函数,可以在频域和时域之间实现平滑过渡,提高音频信号的质量。
4、金融领域:权函数可用于计算资产的加权平均收益率等财务指标,以更准确地反映不同资产对投资组合的贡献程度,权函数还可用于计算风险价值等风险管理指标。
案例分析
以销售数据分析为例,假设我们需要分析一组销售数据,其中不同产品的销售量和销售额之间存在差异,为了更准确地分析销售情况,我们可以引入权函数来计算加权平均值和加权销售额等指标,我们确定不同产品的权重因子(如销售额占比),然后根据权重因子计算每个产品的权函数值,通过计算加权平均值和加权销售额等指标,我们可以更准确地了解销售情况并制定相应的销售策略。
本文介绍了权函数的基本概念、计算方法以及在数据分析、机器学习、信号处理、金融等领域的应用价值,通过案例分析可以看出,引入权函数可以更加准确地描述数据集中各数据点的实际价值,提高分析的准确性和模型的性能,在实际应用中,权函数具有重要的价值。
参考文献
本文参考了一些相关的学术论文和书籍,以介绍和分析权函数的计算方法和应用实例,由于篇幅限制,无法列出所有参考文献,但读者可以通过相关渠道获取更多关于权函数的详细信息,以深入了解其理论和实践价值。


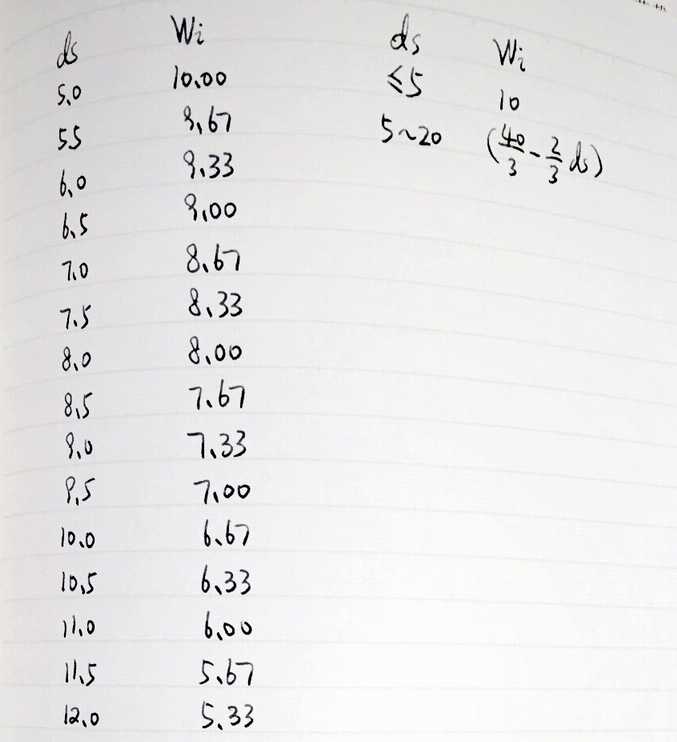
 渝ICP备2020014236号-1
渝ICP备2020014236号-1